相関係数から散布図を作りたい
任意の相関係数\(r\)から,それらしい散布図を作ろうと考えました。
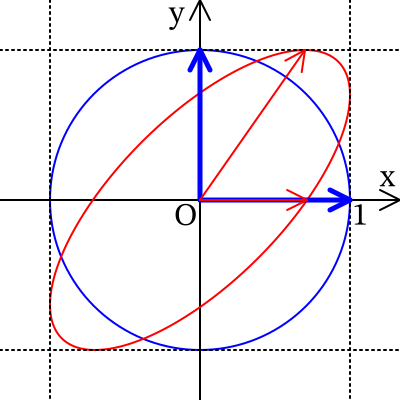
思いついたのが,半径\(1\)の円を基底変換して,いい感じの形を作ればいいのではないかと。
\(-1 \leqq x \leqq 1\),\(-1 \leqq y \leqq 1\)の範囲に収めるためには,
\[ \left[ \begin{array}{cc} \sqrt{1 – a^2} & a \\ 0 & 1 \end{array} \right] \]
の\(1\)次変換をすれば良さそうです。
この式は次のように考えました。相関係数が大きくなると上向きのベクトルが右上の方に変化すると考えて,右方向に動く量を\(a\)とすれば,
\[ \left[ \begin{array}{cc} b & a \\ 0 & 1 \end{array} \right] \left[ \begin{array}{c} \cos \theta \\ \sin \theta \end{array} \right] = \left[ \begin{array}{c} b \cos \theta + a \sin \theta \\ \sin \theta \end{array} \right] \]
の変換を考えて,\(y\)座標は必ず\(-1 \leqq y \leqq 1\)になるから,問題は\(x\)座標で,
\[b \cos \theta + a \sin \theta = \sqrt{a^2 + b^2} \left( \cos \theta \cdot \dfrac{b}{\sqrt{a^2 + b^2}} + \sin \theta \cdot \dfrac{a}{\sqrt{a^2 + b^2}} \right) \]
となるから,
\[ \cos \alpha = \dfrac{b}{\sqrt{a^2 + b^2}}, \sin \alpha = \dfrac{a}{\sqrt{a^2 + b^2}} \]
と置けば,
\[ b \cos \theta + a \sin \theta = \sqrt{a^2 + b^2} \cos(\theta-\alpha) \]
なので,
\[ -\sqrt{a^2 + b^2} \leqq b \cos \theta + a \sin \theta \leqq \sqrt{a^2 + b^2} \]
これより,\(\sqrt{a^2 + b^2} = 1 \)であるから,\(a^2 + b^2 = 1\)なので,
\[ b = \sqrt{1-a^2}\]
これより,媒介変数表示で表すと,次のようになります。\(t\)の範囲は\(0 \leqq t \leqq 2\pi \)
\[ \left\{ \begin{array}{l} x = \sqrt{1-a^2}\cos t + a\sin t \\ y = \sin t \end{array} \right. \]
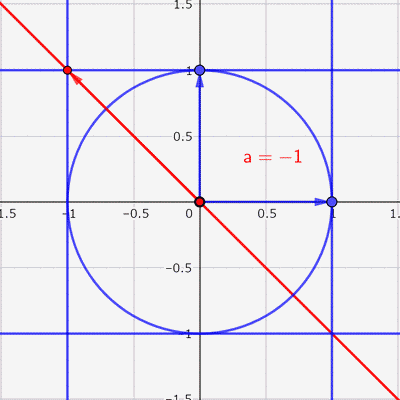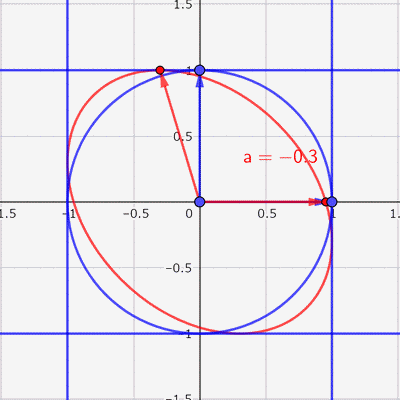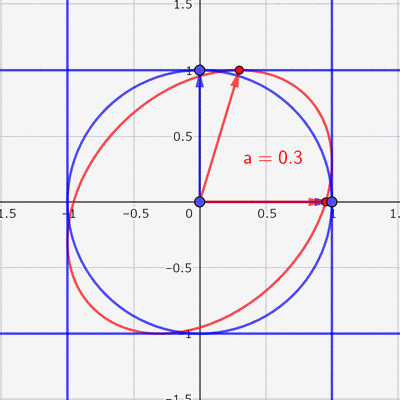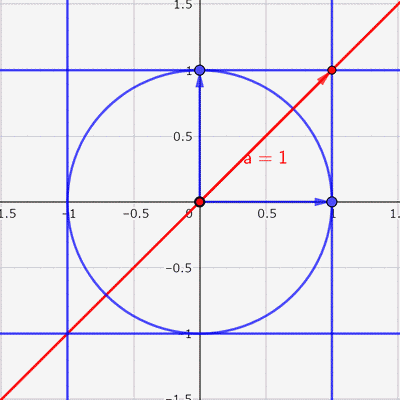
あとは,この赤い楕円の中に点をランダムに打てば,いい感じの散布図ができそうです。
相関係数が\(a\)と同じだったらうれしいなと思って,計算してみました。
この赤い楕円に囲まれた部分にランダムに点を打つことを考えます。横軸をX,縦軸をYとして,Xの分散,Yの分散,XとYの共分散を求めていきます。まず,赤い楕円に囲まれた部分の面積は,青い円を横に\(\sqrt{1-a^2}\)倍しただけなので,
\[\pi\sqrt{1-a^2}\]
です。また,さきほどの媒介変数表示の式を陽関数に変換してみると,
\[ \begin{array}{l} y(x) = ax \pm \sqrt{1-a^2}\sqrt{1-x^2} \\ x(y) = ay \pm \sqrt{1-a^2}\sqrt{1-y^2} \end{array} \]
と表すことができるので,
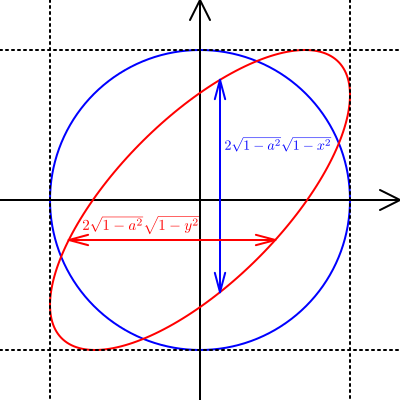
\(x\)方向と\(y\)方向でそれぞれの幅\(w_x(y)\),\(w_y(x)\)を調べると,
\[ \begin{array}{l} w_x(y) = 2\sqrt{1-a^2}\sqrt{1-y^2} \\ w_y(x) = 2\sqrt{1-a^2}\sqrt{1-x^2} \end{array} \]
ですから,XとYの確率密度関数\(f_x(x)\),\(f_y(y)\)は,これらの値を面積で割ることで,
\[ \begin{array}{l} f_x(x) = \dfrac{2\sqrt{1-a^2}\sqrt{1-x^2}}{\pi\sqrt{1-a^2}} = \dfrac{2}{\pi}\sqrt{1-x^2} \\ f_y(y) = \dfrac{2\sqrt{1-a^2}\sqrt{1-y^2}}{\pi\sqrt{1-a^2}} = \dfrac{2}{\pi}\sqrt{1-y^2} \end{array} \]
のように求めることができます。つまり,どちらも\(g(t) = \dfrac{2}{\pi}\sqrt{1-t^2}\)と表せます。
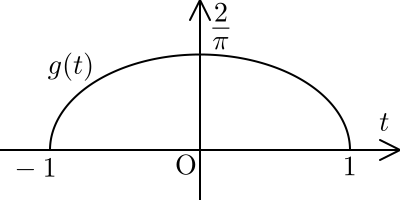
よって,分散は,
\[ \begin{array}{rl}
E[X] & = E[Y] = \displaystyle \int_{-1}^1 xg(x) dx = 0 \\
V[X] & = V[Y] = E[(X-0)^2]=E[X^2] = \displaystyle \int_{-1}^1 x^2g(x) dx \\
& = \displaystyle \dfrac{2}{\pi} \int_{-1}^1 x^2\sqrt{1-x^2} dx \\
& = \displaystyle \dfrac{2}{\pi} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin^2\theta \cos \theta \cdot \cos \theta d\theta \\
& = \displaystyle \dfrac{2}{\pi} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \dfrac{1}{4} \sin^2 2\theta d\theta \\
& = \displaystyle \dfrac{1}{2\pi} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \dfrac{1-\cos 4\theta}{2} d\theta \\
& = \displaystyle \dfrac{1}{4\pi} \left[ \theta-\dfrac{1}{4}\sin 4\theta \right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \\
& = \dfrac{1}{4\pi} \left\{ \dfrac{\pi}{2} – \left( \dfrac{\pi}{2} \right) \right\} = \dfrac{1}{4}
\end{array}\]
のように計算できます。また,同時確率密度関数\( f_{xy}(x,y) \)は,
\( -1 \leqq x \leqq 1, ax-\sqrt{1-a^2}\sqrt{1-x^2} \leqq y \leqq ax+\sqrt{1-a^2}\sqrt{1-x^2} \)の範囲で\(\dfrac{1}{\pi\sqrt{1-a^2}}\),
それ以外で\(0\)をとる関数なので,共分散は
\[ \begin{array}{rl}
Cov(X,Y) & = E[(X-E[X])(Y-E[Y])] = E[XY] \\
& = \displaystyle \int_{-1}^1 \int_{ax-\sqrt{1-a^2}\sqrt{1-x^2}}^{ax+\sqrt{1-a^2}\sqrt{1-x^2}} xy \cdot \dfrac{1}{\pi\sqrt{1-a^2}} dy dx \\
& = \displaystyle \dfrac{1}{\pi\sqrt{1-a^2}} \int_{-1}^1 x \left[ \dfrac{1}{2}y^2 \right]_{ax-\sqrt{1-a^2}\sqrt{1-x^2}}^{ax+\sqrt{1-a^2}\sqrt{1-x^2}} dx \\
& = \displaystyle \dfrac{1}{\pi\sqrt{1-a^2}} \int_{-1}^1 x \cdot 2ax\sqrt{1-a^2}\sqrt{1-x^2} dx \\
& = \displaystyle \dfrac{2a}{\pi} a \int_{-1}^1 x^2\sqrt{1-x^2} dx \\
& = \dfrac{2a}{\pi} \cdot \dfrac{\pi}{8} = \dfrac{a}{4}
\end{array} \]
したがって,相関係数\(r\)は,
\[r = \dfrac{Cov(X,Y)}{\sqrt{V[X] \cdot V[Y]}} = \dfrac{\frac{a}{4}}{\sqrt{\frac{a}{4} \cdot \frac{a}{4}}} = a\]
となります。
実際に作ってみると,\(r=0.7\)の場合は,

こんな感じになりました。ただ,点の数が少ないので,相関係数の値が結構ぶれてしまいます。試行回数を増やせば,目的の散布図は作成できそうです。