難問の積分を解いてみた
問題 \( I=\displaystyle \int_{-\frac{1}{2}}^{\frac{1}{2}} \sqrt{x^2+1+\sqrt{x^4+x^2+1}} \> dx \)を求めよ。
まず,
\[ \begin{array}{r@{\>}l}
x^4+x^2+1 & =x^4+2x^2+1-x^2 \\
& = (x^2+1)^2-x^2 \\
& = \{ (x^2 + 1)+x \}\{ (x^2 + 1)-x \} \\
& = (x^2+x+1)(x^2-x+1)
\end{array} \]
と変形できるので,
\[ \displaystyle I=\int_{-\frac{1}{2}}^{\frac{1}{2}} \sqrt{x^2+1+\sqrt{(x^2+x+1)(x^2-x+1)}} \> dx \]
二重根号を外すことを考えて,
\[ \begin{array}{rl}
I & \displaystyle =\int_{-\frac{1}{2}}^{\frac{1}{2}} \dfrac{\sqrt{2x^2+2+2\sqrt{(x^2+x+1)(x^2-x+1)}}}{\sqrt{2}} \> dx \\
& \displaystyle = \dfrac{1}{\sqrt{2}} \int_{-\frac{1}{2}}^{\frac{1}{2}} \sqrt{(x^2+x+1)+(x^2-x+1)+2\sqrt{(x^2+x+1)(x^2-x+1)}} \> dx \\
& \displaystyle = \dfrac{1}{\sqrt{2}} \int_{-\frac{1}{2}}^{\frac{1}{2}} (\sqrt{x^2+x+1}+\sqrt{x^2-x+1}) \> dx \\
& \displaystyle = \dfrac{1}{\sqrt{2}} \left( \int_{-\frac{1}{2}}^{\frac{1}{2}} \sqrt{x^2+x+1} \> dx + \int_{-\frac{1}{2}}^{\frac{1}{2}} \sqrt{x^2-x+1}) \> dx \right) \\
\end{array}\]
ここで,ルートの中の平方完成を考えて,
\[ \begin{array}{rl}
I & \displaystyle = \dfrac{1}{\sqrt{2}} \left\{ \int_{-\frac{1}{2}}^{\frac{1}{2}} \sqrt{ \left( x + \dfrac{1}{2} \right)^2+\dfrac{3}{4}} \> dx+\int_{-\frac{1}{2}}^{\frac{1}{2}} \sqrt{ \left( x-\dfrac{1}{2} \right)^2+\dfrac{3}{4}} \> dx \right\} \\
\end{array}\]
ここで,\(x+\dfrac{1}{2}=\dfrac{\sqrt{3}}{2}\tan{\theta_1}\),\(x-\dfrac{1}{2}=\dfrac{\sqrt{3}}{2}\tan{\theta_2}\)とする。
また,\(\tan t = \dfrac{2}{\sqrt{3}} \left(0 \leqq t \leqq \dfrac{\pi}{2}\right)\)を満たす \( t \) を \(\alpha\) とすると,
\[\begin{array}{rl}
\dfrac{dx}{d\theta_1} & = \dfrac{\sqrt{3}}{2}\dfrac{1}{\cos^2\theta_1} \\
\dfrac{dx}{d\theta_2} & = \dfrac{\sqrt{3}}{2}\dfrac{1}{\cos^2\theta_2}
\end{array}\]
\[\begin{array}{c|ccc}
x & -\dfrac{1}{2} & \rightarrow & \dfrac{1}{2} \\ \hline
\theta_1 & 0 & \rightarrow & \alpha
\end{array} \hspace{5mm}
\begin{array}{c|ccc}
x & -\dfrac{1}{2} & \rightarrow & \dfrac{1}{2} \\ \hline
\theta_2 & -\alpha & \rightarrow & 0
\end{array}\]
となるので,
\[ \begin{array}{rl}
I & \displaystyle = \dfrac{1}{\sqrt{2}} \left( \int_{-\frac{1}{2}}^{\frac{1}{2}} \sqrt{ \dfrac{3}{4}\tan^2\theta_1+\dfrac{3}{4}} \> dx+\int_{-\frac{1}{2}}^{\frac{1}{2}} \sqrt{ \dfrac{3}{4}\tan^2\theta_2+\dfrac{3}{4}} \> dx \right) \\
& \displaystyle = \dfrac{1}{\sqrt{2}} \left( \int_{-\frac{1}{2}}^{\frac{1}{2}} \dfrac{\sqrt{3}}{2}\sqrt{1+\tan^2\theta_1} \> dx+\int_{-\frac{1}{2}}^{\frac{1}{2}} \dfrac{\sqrt{3}}{2}\sqrt{1+\tan^2\theta_2} \> dx \right) \\
& \displaystyle = \dfrac{\sqrt{3}}{2\sqrt{2}} \left( \int_{-\frac{1}{2}}^{\frac{1}{2}} \sqrt{\dfrac{1}{\cos^2\theta_1}} \> dx+\int_{-\frac{1}{2}}^{\frac{1}{2}} \sqrt{\dfrac{1}{\cos^2\theta_2}} \> dx \right) \\
& \displaystyle = \dfrac{\sqrt{3}}{2\sqrt{2}} \left( \int_{-\frac{1}{2}}^{\frac{1}{2}} \dfrac{1}{\cos\theta_1} \> dx+\int_{-\frac{1}{2}}^{\frac{1}{2}} \dfrac{1}{\cos\theta_2} \> dx \right) \\
& \displaystyle = \dfrac{\sqrt{3}}{2\sqrt{2}} \left( \int_{0}^{\alpha} \dfrac{1}{\cos\theta_1} \dfrac{\sqrt{3}}{2}\dfrac{d\theta_1}{\cos^2\theta_1}+\int_{-\alpha}^{0} \dfrac{1}{\cos\theta_2} \dfrac{\sqrt{3}}{2}\dfrac{d\theta_2}{\cos^2\theta_2} \right) \\
& \displaystyle = \dfrac{3}{4\sqrt{2}} \left( \int_{0}^{\alpha} \dfrac{d\theta_1}{\cos^3\theta_1}+\int_{-\alpha}^{0} \dfrac{d\theta_2}{\cos^3\theta_2} \right) \\
& \displaystyle = \dfrac{3}{4\sqrt{2}} \int_{-\alpha}^{\alpha} \dfrac{d\theta}{\cos^3\theta} \\
& \displaystyle = \dfrac{3}{2\sqrt{2}} \int_{0}^{\alpha} \dfrac{d\theta}{\cos^3\theta} \\
\end{array} \]
ここで,\(\dfrac{1}{\cos^3\theta}\)の不定積分を考える。
\[\begin{array}{rl}
\displaystyle \int \dfrac{d\theta}{\cos^3\theta}
& \displaystyle =\int \dfrac{1}{\cos^2\theta} \dfrac{1}{\cos\theta} d\theta \\
& \displaystyle =\int (\tan\theta)’\dfrac{1}{\cos\theta} d\theta \\
& \displaystyle = \dfrac{\tan\theta}{\cos\theta}-\int \tan\theta \left( \dfrac{1}{\cos\theta} \right)’ d\theta \\
& \displaystyle = \dfrac{\tan\theta}{\cos\theta}-\int \tan\theta \dfrac{\tan\theta}{\cos\theta} d\theta \\
& \displaystyle = \dfrac{\tan\theta}{\cos\theta}-\int \tan^2\theta \dfrac{1}{\cos\theta} d\theta \\
& \displaystyle = \dfrac{\tan\theta}{\cos\theta}-\int \left( \dfrac{1}{\cos^2\theta}-1 \right) \dfrac{1}{\cos\theta} d\theta \\
& \displaystyle = \dfrac{\tan\theta}{\cos\theta}-\int \dfrac{1}{\cos^3\theta} \> d\theta + \int \dfrac{1}{\cos\theta} \> d\theta \\
\end{array}\]
\[\begin{array}{rl}
\displaystyle 2\int \dfrac{1}{\cos^3\theta} \> d\theta
& \displaystyle = \dfrac{\tan\theta}{\cos\theta}+\int \dfrac{1}{\cos\theta} \> d\theta \\
\displaystyle \int \dfrac{1}{\cos^3\theta} \> d\theta
& \displaystyle = \dfrac{1}{2}\dfrac{\tan\theta}{\cos\theta}+\dfrac{1}{2}\int \dfrac{1}{\cos\theta} \> d\theta
\end{array}\]
さらに,\(\dfrac{1}{\cos\theta}\)の不定積分を考えると,
\[\begin{array}{rl}
\displaystyle \int \dfrac{d\theta}{\cos\theta}
& \displaystyle = \int \dfrac{\cos\theta}{\cos^2\theta} \> d\theta \\
& \displaystyle = \int \dfrac{\cos\theta}{1-\sin^2\theta} \> d\theta \\
& \displaystyle = \int \dfrac{\cos\theta}{(1+\sin\theta)(1-\sin\theta)} \> d\theta \\
& \displaystyle = \int \dfrac{1}{2} \left( \dfrac{\cos\theta}{1+\sin\theta} + \dfrac{\cos\theta}{1-\sin\theta}\right) \> d\theta \\
& \displaystyle = \dfrac{1}{2} \int \left( \dfrac{(1+\sin\theta)’}{1+\sin\theta}-\dfrac{(1-\sin\theta)’}{1-\sin\theta} \right) \> d\theta \\
& \displaystyle = \dfrac{1}{2} \left( \log|1+\sin\theta|-\log|1-\sin\theta| \right)+C \\
& \displaystyle = \dfrac{1}{2} \log\dfrac{1+\sin\theta}{1-\sin\theta}+C
\end{array}\]
なので,
\[\begin{array}{rl}
\displaystyle \int \dfrac{1}{\cos^3\theta} \> d\theta
& \displaystyle = \dfrac{1}{2}\dfrac{\tan\theta}{\cos\theta}+\dfrac{1}{4}\log\dfrac{1+\sin\theta}{1-\sin\theta}+C
\end{array}\]
\(\tan\alpha=\dfrac{2}{\sqrt{3}}\)より\(\sin\alpha=\dfrac{2}{\sqrt{7}}\),\(\cos\alpha=\dfrac{\sqrt{3}}{\sqrt{7}}\)なので,
\[\begin{array}{rl}
I & \displaystyle = \dfrac{3}{2\sqrt{2}} \int_{0}^{\alpha} \dfrac{d\theta}{\cos^3\theta} \\
& =\dfrac{3}{2\sqrt{2}} \left[ \dfrac{1}{2}\dfrac{\tan\theta}{\cos\theta}+\dfrac{1}{4}\log\dfrac{1+\sin\theta}{1-\sin\theta} \right]_0^\alpha \\
& =\dfrac{3}{2\sqrt{2}} \left\{ \left( \dfrac{1}{2}\dfrac{2}{\sqrt{3}}\dfrac{\sqrt{7}}{\sqrt{3}}+\dfrac{1}{4}\log\dfrac{1+\frac{2}{\sqrt{7}}}{1-\frac{2}{\sqrt{7}}} \right)-0 \right\} \\
& =\dfrac{3}{2\sqrt{2}} \left( \dfrac{\sqrt{7}}{3}+\dfrac{1}{4}\log\dfrac{\sqrt{7}+2}{\sqrt{7}-2} \right) \\
& =\dfrac{\sqrt{14}}{4}+\dfrac{3\sqrt{2}}{16}\log\dfrac{\sqrt{7}+2}{\sqrt{7}-2}
\end{array}\]
問題は次の動画から。自分でも解いてみたので解答を残すことにしました。
\( \displaystyle \int_{-\frac{1}{2}}^{\frac{1}{2}} \sqrt{\left( x+\dfrac{1}{2} \right)^2+\dfrac{3}{4}} dx\)からの変数変換で,\(y=x+\dfrac{1}{2}\)とおいて,\(y+\sqrt{y^2+\dfrac{3}{4}} = t\)とするのは初めて見た気がするので,覚えておこうと思います。
\[\begin{array}{rl}
y+\sqrt{y^2+\dfrac{3}{4}} & =t \\
\sqrt{y^2+\dfrac{3}{4}} & =t-y \\
y^2+\dfrac{3}{4} & =t^2-2ty+y^2 \\
2ty & =t^2-\dfrac{3}{4} \\
8ty & =4t^2-3 \\
y & =\dfrac{4t^2-3}{8t} \\
\dfrac{dy}{dt} & = \dfrac{8t \cdot 8t-(4t^2-3) \cdot 8}{64t^2} \\
&= \dfrac{8t^2-4t^2+3}{8t^2} \\
&= \dfrac{4t^2+3}{8t^2} \\
\end{array}\]
となるから,
\[\begin{array}{rl}
\displaystyle \int_{-\frac{1}{2}}^{\frac{1}{2}} \sqrt{\left( x+\dfrac{1}{2} \right)^2+\dfrac{3}{4}} dx
& \displaystyle = \int_0^1 \sqrt{y^2+\dfrac{3}{4}} \> dy \\
& \displaystyle = \int_{0}^{1} (t-y) dy \\
& \displaystyle = \int_{\frac{\sqrt{3}}{2}}^{1+\frac{\sqrt{7}}{2}} \left( t-\dfrac{4t^2-3}{8t} \right) \dfrac{4t^2+3}{8t^2} dt \\
& \displaystyle = \int_{\frac{\sqrt{3}}{2}}^{1+\frac{\sqrt{7}}{2}} \dfrac{4t^2+3}{8t} \dfrac{4t^2+3}{8t^2} dt \\
& \displaystyle = \int_{\frac{\sqrt{3}}{2}}^{1+\frac{\sqrt{7}}{2}} \dfrac{(4t^2+3)^2}{64t^3} dt \\
& \displaystyle = \int_{\frac{\sqrt{3}}{2}}^{1+\frac{\sqrt{7}}{2}} \dfrac{16t^4+24t^2+9}{64t^3} dt \\
& \displaystyle = \dfrac{1}{64} \int_{\frac{\sqrt{3}}{2}}^{1+\frac{\sqrt{7}}{2}} (16t+24t^{-1}+9t^{-3}) dt \\
& \displaystyle = \dfrac{1}{64} \left[ 8t^2+24\log|t|-\dfrac{9}{2}t^{-2} \right]_{\frac{\sqrt{3}}{2}}^{1+\frac{\sqrt{7}}{2}} \\
& = \cdots \\
& = \dfrac{\sqrt{7}}{4}+\dfrac{3}{8}\log\dfrac{2+\sqrt{7}}{\sqrt{3}}
\end{array}\]
式は複雑ですが,三角関数を経由しないのがいいですね。
相関係数から散布図を作りたい
任意の相関係数\(r\)から,それらしい散布図を作ろうと考えました。
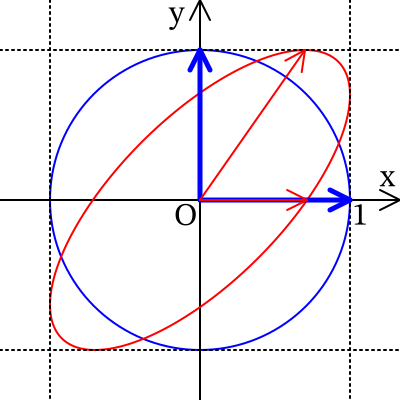
思いついたのが,半径\(1\)の円を基底変換して,いい感じの形を作ればいいのではないかと。
\(-1 \leqq x \leqq 1\),\(-1 \leqq y \leqq 1\)の範囲に収めるためには,
\[ \left[ \begin{array}{cc} \sqrt{1 – a^2} & a \\ 0 & 1 \end{array} \right] \]
の\(1\)次変換をすれば良さそうです。
この式は次のように考えました。相関係数が大きくなると上向きのベクトルが右上の方に変化すると考えて,右方向に動く量を\(a\)とすれば,
\[ \left[ \begin{array}{cc} b & a \\ 0 & 1 \end{array} \right] \left[ \begin{array}{c} \cos \theta \\ \sin \theta \end{array} \right] = \left[ \begin{array}{c} b \cos \theta + a \sin \theta \\ \sin \theta \end{array} \right] \]
の変換を考えて,\(y\)座標は必ず\(-1 \leqq y \leqq 1\)になるから,問題は\(x\)座標で,
\[b \cos \theta + a \sin \theta = \sqrt{a^2 + b^2} \left( \cos \theta \cdot \dfrac{b}{\sqrt{a^2 + b^2}} + \sin \theta \cdot \dfrac{a}{\sqrt{a^2 + b^2}} \right) \]
となるから,
\[ \cos \alpha = \dfrac{b}{\sqrt{a^2 + b^2}}, \sin \alpha = \dfrac{a}{\sqrt{a^2 + b^2}} \]
と置けば,
\[ b \cos \theta + a \sin \theta = \sqrt{a^2 + b^2} \cos(\theta-\alpha) \]
なので,
\[ -\sqrt{a^2 + b^2} \leqq b \cos \theta + a \sin \theta \leqq \sqrt{a^2 + b^2} \]
これより,\(\sqrt{a^2 + b^2} = 1 \)であるから,\(a^2 + b^2 = 1\)なので,
\[ b = \sqrt{1-a^2}\]
これより,媒介変数表示で表すと,次のようになります。\(t\)の範囲は\(0 \leqq t \leqq 2\pi \)
\[ \left\{ \begin{array}{l} x = \sqrt{1-a^2}\cos t + a\sin t \\ y = \sin t \end{array} \right. \]
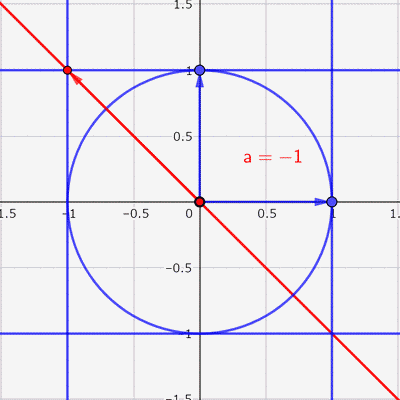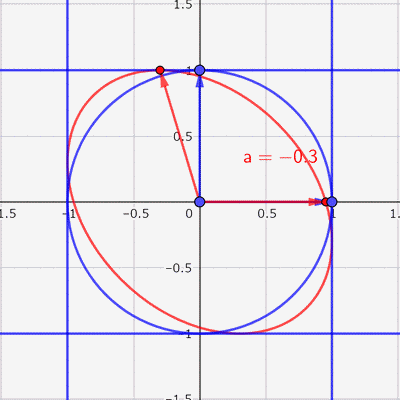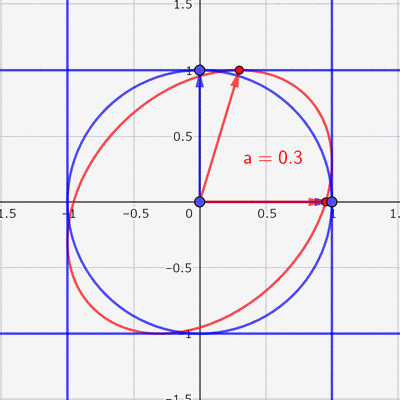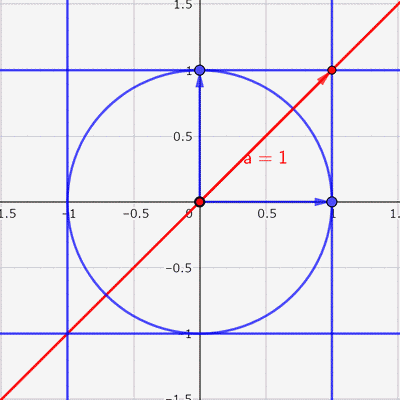
あとは,この赤い楕円の中に点をランダムに打てば,いい感じの散布図ができそうです。
相関係数が\(a\)と同じだったらうれしいなと思って,計算してみました。
この赤い楕円に囲まれた部分にランダムに点を打つことを考えます。横軸をX,縦軸をYとして,Xの分散,Yの分散,XとYの共分散を求めていきます。まず,赤い楕円に囲まれた部分の面積は,青い円を横に\(\sqrt{1-a^2}\)倍しただけなので,
\[\pi\sqrt{1-a^2}\]
です。また,さきほどの媒介変数表示の式を陽関数に変換してみると,
\[ \begin{array}{l} y(x) = ax \pm \sqrt{1-a^2}\sqrt{1-x^2} \\ x(y) = ay \pm \sqrt{1-a^2}\sqrt{1-y^2} \end{array} \]
と表すことができるので,
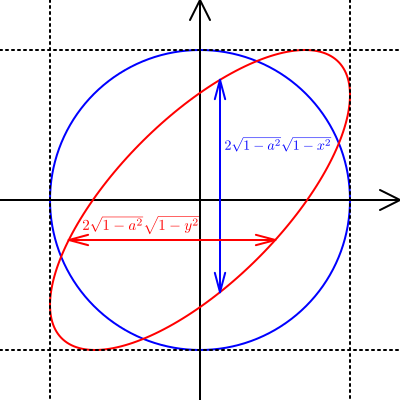
\(x\)方向と\(y\)方向でそれぞれの幅\(w_x(y)\),\(w_y(x)\)を調べると,
\[ \begin{array}{l} w_x(y) = 2\sqrt{1-a^2}\sqrt{1-y^2} \\ w_y(x) = 2\sqrt{1-a^2}\sqrt{1-x^2} \end{array} \]
ですから,XとYの確率密度関数\(f_x(x)\),\(f_y(y)\)は,これらの値を面積で割ることで,
\[ \begin{array}{l} f_x(x) = \dfrac{2\sqrt{1-a^2}\sqrt{1-x^2}}{\pi\sqrt{1-a^2}} = \dfrac{2}{\pi}\sqrt{1-x^2} \\ f_y(y) = \dfrac{2\sqrt{1-a^2}\sqrt{1-y^2}}{\pi\sqrt{1-a^2}} = \dfrac{2}{\pi}\sqrt{1-y^2} \end{array} \]
のように求めることができます。つまり,どちらも\(g(t) = \dfrac{2}{\pi}\sqrt{1-t^2}\)と表せます。
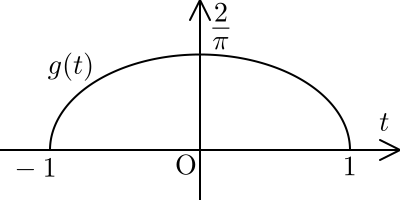
よって,分散は,
\[ \begin{array}{rl}
E[X] & = E[Y] = \displaystyle \int_{-1}^1 xg(x) dx = 0 \\
V[X] & = V[Y] = E[(X-0)^2]=E[X^2] = \displaystyle \int_{-1}^1 x^2g(x) dx \\
& = \displaystyle \dfrac{2}{\pi} \int_{-1}^1 x^2\sqrt{1-x^2} dx \\
& = \displaystyle \dfrac{2}{\pi} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin^2\theta \cos \theta \cdot \cos \theta d\theta \\
& = \displaystyle \dfrac{2}{\pi} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \dfrac{1}{4} \sin^2 2\theta d\theta \\
& = \displaystyle \dfrac{1}{2\pi} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \dfrac{1-\cos 4\theta}{2} d\theta \\
& = \displaystyle \dfrac{1}{4\pi} \left[ \theta-\dfrac{1}{4}\sin 4\theta \right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \\
& = \dfrac{1}{4\pi} \left\{ \dfrac{\pi}{2} – \left( \dfrac{\pi}{2} \right) \right\} = \dfrac{1}{4}
\end{array}\]
のように計算できます。また,同時確率密度関数\( f_{xy}(x,y) \)は,
\( -1 \leqq x \leqq 1, ax-\sqrt{1-a^2}\sqrt{1-x^2} \leqq y \leqq ax+\sqrt{1-a^2}\sqrt{1-x^2} \)の範囲で\(\dfrac{1}{\pi\sqrt{1-a^2}}\),
それ以外で\(0\)をとる関数なので,共分散は
\[ \begin{array}{rl}
Cov(X,Y) & = E[(X-E[X])(Y-E[Y])] = E[XY] \\
& = \displaystyle \int_{-1}^1 \int_{ax-\sqrt{1-a^2}\sqrt{1-x^2}}^{ax+\sqrt{1-a^2}\sqrt{1-x^2}} xy \cdot \dfrac{1}{\pi\sqrt{1-a^2}} dy dx \\
& = \displaystyle \dfrac{1}{\pi\sqrt{1-a^2}} \int_{-1}^1 x \left[ \dfrac{1}{2}y^2 \right]_{ax-\sqrt{1-a^2}\sqrt{1-x^2}}^{ax+\sqrt{1-a^2}\sqrt{1-x^2}} dx \\
& = \displaystyle \dfrac{1}{\pi\sqrt{1-a^2}} \int_{-1}^1 x \cdot 2ax\sqrt{1-a^2}\sqrt{1-x^2} dx \\
& = \displaystyle \dfrac{2a}{\pi} a \int_{-1}^1 x^2\sqrt{1-x^2} dx \\
& = \dfrac{2a}{\pi} \cdot \dfrac{\pi}{8} = \dfrac{a}{4}
\end{array} \]
したがって,相関係数\(r\)は,
\[r = \dfrac{Cov(X,Y)}{\sqrt{V[X] \cdot V[Y]}} = \dfrac{\frac{a}{4}}{\sqrt{\frac{a}{4} \cdot \frac{a}{4}}} = a\]
となります。
実際に作ってみると,\(r=0.7\)の場合は,

こんな感じになりました。ただ,点の数が少ないので,相関係数の値が結構ぶれてしまいます。試行回数を増やせば,目的の散布図は作成できそうです。
2nCn/2が奇数となるnを求めよ
問題 \(\dfrac{{}_{2n}{\rm C}_n}{2}\)が奇数となる\(n\)をすべて求めよ。
\({}_{2n}{\rm C}_n = \dfrac{(2n)!}{n!n!}\)と表せるので,\(\dfrac{{}_{2n}{\rm C}_n}{2}\)が奇数となるには,\((2n)!\)に含まれる素因数\(2\)の数から\((n!)^2\)に含まれる素因数\(2\)の数を引いて\(1\)となればよい。
つまり,\(v(m)\)を\(m\)に含まれる素因数\(2\)の数を表す関数とすると,$$v((2n)!) – 2v(n!) = 1$$が成り立てばよい。
ここで,\(v(m!)\)は,$$\begin{array}{r@{\>}l} v(m!) & = \left\lfloor \dfrac{m}{2} \right\rfloor + \left\lfloor \dfrac{m}{4} \right\rfloor + \left\lfloor \dfrac{m}{2^3} \right\rfloor + \cdots + \left\lfloor \dfrac{m}{2^i} \right\rfloor + \cdots \\ & = \displaystyle \sum_{i = 1}^\infty \left\lfloor \dfrac{m}{2^i} \right\rfloor \end{array}$$と計算できる。
整数\(m_1, m_2, \cdots, m_k\)\((m_1 > m_2 > \cdots >m_k)\)を用いて,
\( n = 2^{m_1} + 2^{m_2} + \cdots + 2^{m_k} \)とすると,$$v(n!) = \displaystyle \sum_{i=1}^\infty \left\lfloor \dfrac{2^{m_1} + 2^{m_2} + \cdots + 2^{m_k}}{2^i} \right\rfloor $$と表せる。
ここで,\(m_1>m_2>\cdots>m_s \geq i > m_t > \cdots > m_k \)となるとき,
\(2^{m_t}+2^{m_{t+1}}+\cdots+2^{k-1}+2^k<2^i\)なので,\(\dfrac{2^{m_t}+2^{m_{t+1}}+\cdots+2^{k}}{2^i} < 1\)であるから,$$ \begin{array}{r@{\>}l} \left\lfloor \dfrac{2^{m_1}+2^{m_2}+\cdots+2^{m_k}}{2^i} \right\rfloor & = 2^{m_1-i}+2^{m_2-i}+\cdots+2^{m_s-i} \\ & = \left\lfloor \dfrac{2^{m_1}}{2^i} \right\rfloor + \left\lfloor \dfrac{2^{m_2}}{2^i} \right\rfloor + \cdots + \left\lfloor \dfrac{2^{m_k}}{2^i} \right\rfloor \end{array} $$と表せるから,
$$\begin{array}{rl} v(n!) & = \displaystyle \sum_{i=1}^\infty \left( \left\lfloor \dfrac{2^{m_1}}{2^i} \right\rfloor + \left\lfloor \dfrac{2^{m_2}}{2^i} \right\rfloor + \cdots + \left\lfloor \dfrac{2^{m_k}}{2^i} \right\rfloor \right) \\ & = \displaystyle \sum_{i=1}^\infty \left\lfloor \dfrac{2^{m_1}}{2^i} \right\rfloor + \sum_{i=1}^\infty \left\lfloor \dfrac{2^{m_2}}{2^i} \right\rfloor + \cdots + \sum_{i=1}^\infty \left\lfloor \dfrac{2^{m_k}}{2^i} \right\rfloor \\ & = (2^{m_1-1}+2^{m_1-2}+\cdots+2^0) + (2^{m_2-1}+2^{m_2-2} +\cdots+2^0) + \cdots \\ & = \dfrac{2^{m_1}-1}{2-1} + \dfrac{2^{m_2}-1}{2 – 1} + \cdots + \dfrac{2^{m_k}-1}{2 – 1} \\ & = 2^{m_1} + 2^{m_2} + \cdots + 2^{m_k} – k \end{array}$$
\(v((2n)!)\)についても,同様に考えると,$$v((2n)!) = 2^{m_1+1} + 2^{m_2+1} + \cdots +2^{m_k+1}-k$$と表せる。
よって,$$\begin{array}{l} v((2n)!) – 2v(n!) \\ = (2^{m_1+1}+\cdots+2^{m_k+1}-k)-2(2^{m_1}+\cdots+2^{m_k+1}-k) \\ = (2^{m_1+1}+\cdots+2^{m_k+1}-k)-(2^{m_1+1}+\cdots+2^{m_k+1}-2k) \\ =k \end{array}$$となる。
したがって,条件を満たすには\(k = 1\)でなければならないから,\(0\)以上の整数\(j\)を使って,\(n=2^j\)と表せるときだけ\(\dfrac{{}_{2n}{\rm C}_n}{2}\)が奇数になる。
この問題は下の動画を見て,ChatGPTで解けるかなと思ってやってみました。最初は\(n=1\)のときのみを答えとしていてうまく答えを出すことはできませんでした。模範解答は\(n=2^j\)だよと教えると,間違っていましたが,それらしい解答を提示するようになりました。上の解答はChatGPTが示した解答を大幅に加筆,修正したものです。
\({}_{2n}{\rm C}_n\)の素因数\(2\)の数が\(n\)を\(2\)進数表記をしたときの\(1\)の数と等しいのは,面白い性質です。ChatGPT(3.5)で数学はできませんが,ChatGPT(4)であれば簡単な問題を解いてくるようになりました。提示してくる解答は正しいとは限りませんが,よいアイデアを出すこともあるので面白いですね。